用一個函數在某一點的各階導數來表示該函數在某點附近的取值的公式。

常用的麥克勞林公式
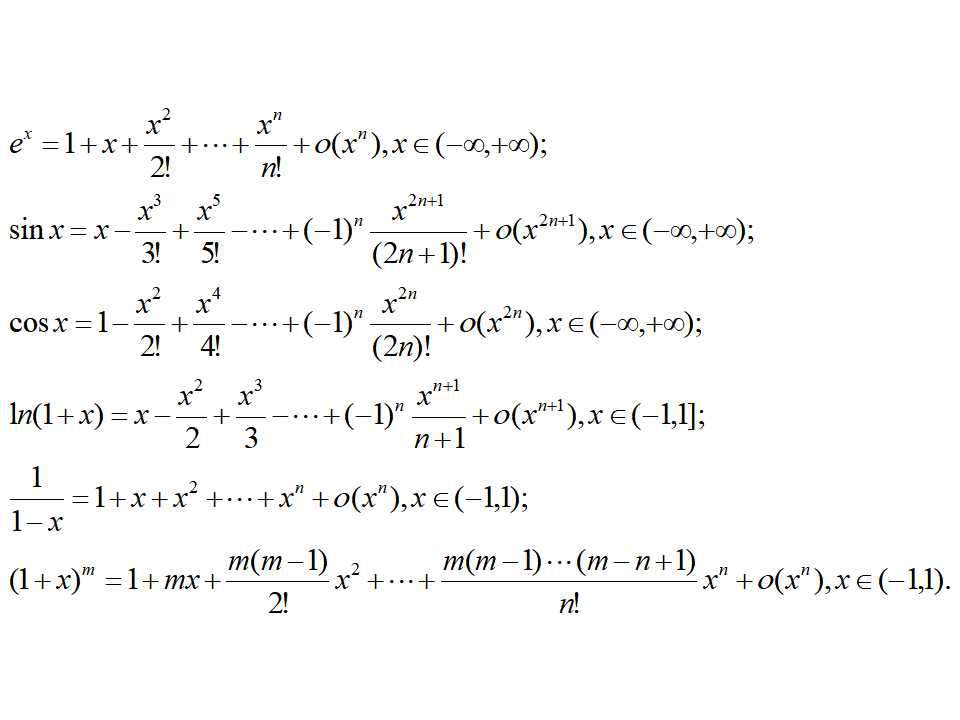
運用第一個麥克勞林公式,當x=1時,我們可以知道常數e=1+1+1/2!+···+1/n!
高階導數
通過上面對泰勒公式和麥克勞林公式的分析,在求一個函數在某點的泰勒公式展開式或者求某一函數的麥克勞林展開式的時候,我們必然需要先求該函數的高階導數。下面簡單地羅列一下比較常用的高階導數公式。
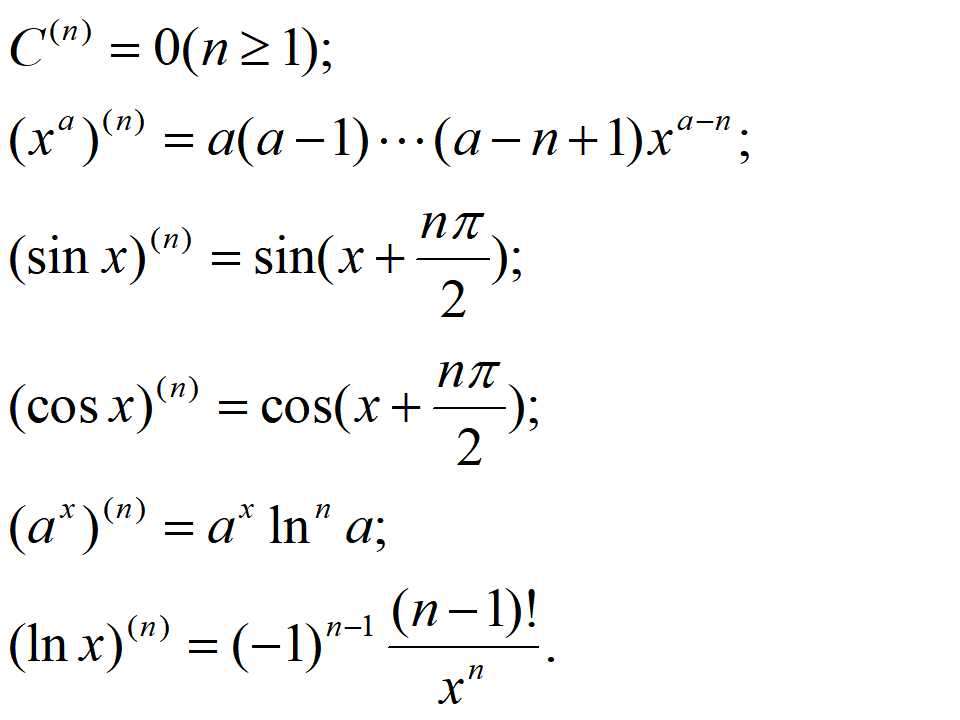
免責聲明:本文內容來自用戶上傳并發布,站點僅提供信息存儲空間服務,不擁有所有權,信息僅供參考之用。
用一個函數在某一點的各階導數來表示該函數在某點附近的取值的公式。

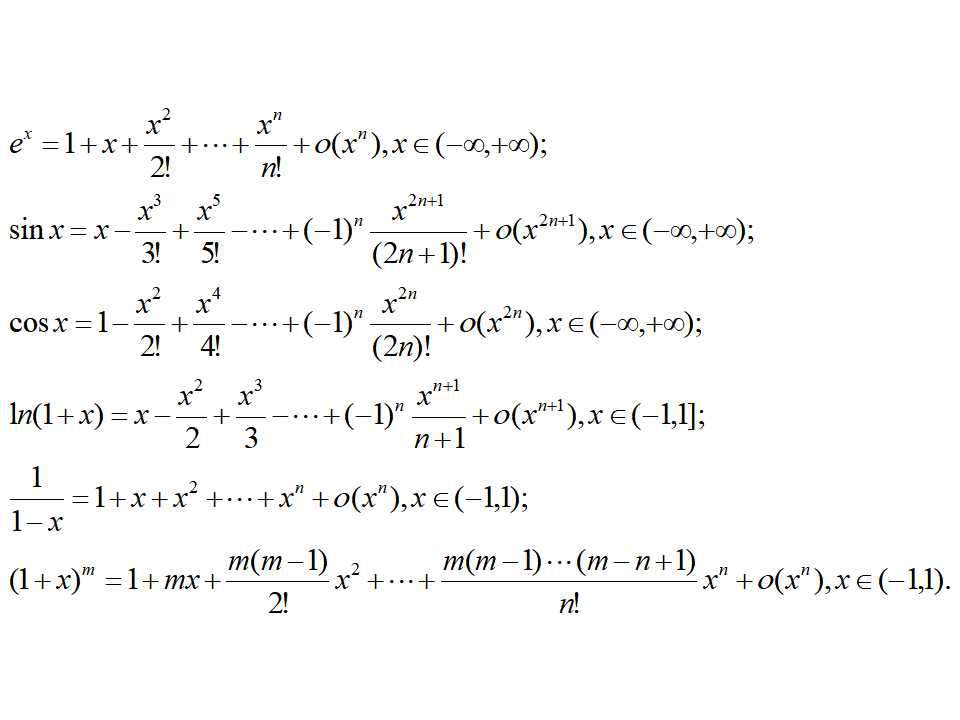
運用第一個麥克勞林公式,當x=1時,我們可以知道常數e=1+1+1/2!+···+1/n!
通過上面對泰勒公式和麥克勞林公式的分析,在求一個函數在某點的泰勒公式展開式或者求某一函數的麥克勞林展開式的時候,我們必然需要先求該函數的高階導數。下面簡單地羅列一下比較常用的高階導數公式。
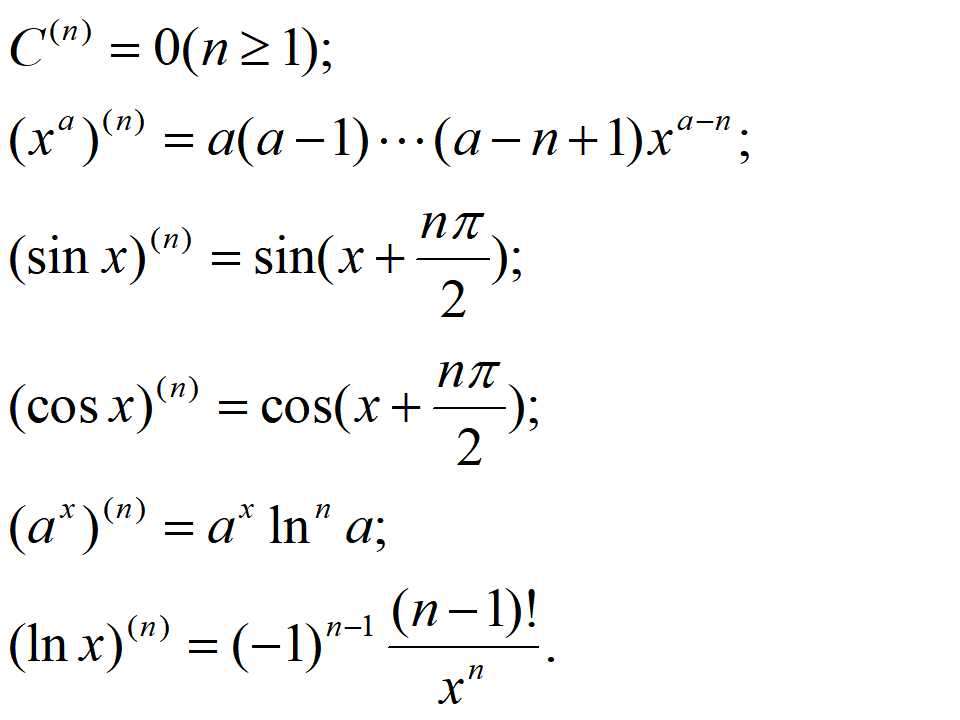
免責聲明:本文內容來自用戶上傳并發布,站點僅提供信息存儲空間服務,不擁有所有權,信息僅供參考之用。